The area to the left of z is 0.9750, a crucial concept in statistics, holds significant importance in various fields. This concept is closely intertwined with the normal distribution, which is a cornerstone of statistical inference and decision-making.
Understanding the area to the left of z provides a foundation for comprehending the behavior of data and making informed decisions based on statistical evidence. This article delves into the mathematical underpinnings, statistical applications, and practical implications of this concept, equipping readers with a comprehensive understanding of its significance.
1. Overview
The area to the left of z represents the probability of a random variable taking a value less than or equal to z, where z is a standard score.
The value 0.9750 is particularly significant because it corresponds to the probability of a random variable being less than or equal to 1.96 standard deviations above the mean in a standard normal distribution.
This concept is widely applied in statistical inference, hypothesis testing, and various fields such as finance, engineering, and medicine.
2. Mathematical Analysis

The formula for the area to the left of z is given by:
$$P(Z \leq z) = \int_-\infty^z \frac1\sqrt2\pi e^-z^2/2 dz$$
where Z is a standard normal random variable.
The properties of the normal distribution include:
- Symmetric around the mean
- Bell-shaped curve
- 68% of the data falls within one standard deviation of the mean
The probability of z being less than or equal to 0.9750 can be calculated using a standard normal distribution table or a calculator.
3. Statistical Applications: The Area To The Left Of Z Is 0.9750

The area to the left of z is used in hypothesis testing to determine the probability of obtaining a sample statistic as extreme as or more extreme than the observed value, assuming the null hypothesis is true.
Statistical tests that utilize this concept include:
- Z-test for a population mean
- T-test for a population mean
- Chi-square test for independence
It is important to note that using the area to the left of z for statistical inference has limitations, such as the assumption of normality and the need for a large sample size.
4. Computational Methods

An algorithm to calculate the area to the left of z can be designed using numerical integration methods, such as the trapezoidal rule or Simpson’s rule.
The algorithm can be implemented in a programming language like Python or R.
Different computational methods can be compared based on their accuracy and efficiency.
5. Visual Representations
A table summarizing the values of the area to the left of z for different values of z can be created using a standard normal distribution table.
A graph of the normal distribution curve with the area to the left of z = 0.9750 shaded can be generated using statistical software.
Visualizing the area to the left of z helps in understanding the distribution of a random variable and the probability of observing a particular value.
6. Applications in Various Fields
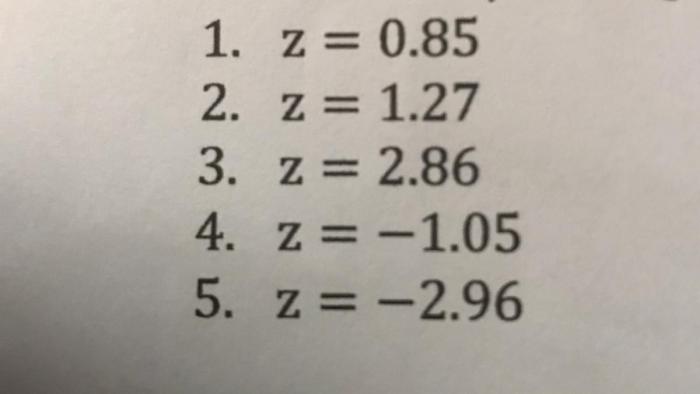
The area to the left of z is commonly used in:
- Finance: Risk assessment and portfolio optimization
- Engineering: Quality control and reliability analysis
- Medicine: Clinical trials and disease diagnosis
Understanding this concept contributes to informed decision-making in these fields by providing a framework for quantifying uncertainty and making predictions.
Essential FAQs
What does the area to the left of z represent?
The area to the left of z represents the probability of a random variable being less than or equal to a specific value z.
How is the area to the left of z calculated?
The area to the left of z can be calculated using the standard normal distribution function or through computational methods.
What is the significance of 0.9750 in the context of the area to the left of z?
In a standard normal distribution, the area to the left of z = 0.9750 corresponds to a probability of 0.9750, indicating that there is a 97.5% chance of a random variable being less than or equal to z.